DERIVADAS DE ORDEN SUPERIOR
La derivada de la derivada de una función se conoce como
segunda derivada de la función, es decir, si f(x) es una función y existe su
primera derivada f´(x), en el caso de que se pueda obtener, la derivada de la
función obtenida de aplicar la derivada se le llama segunda derivada:

de manera similar se puede obtener las derivadas de mayor
orden, sin embargo es necesario aclarar que las derivadas de una función
dependen de las características de la función y es posible, y frecuentemente
sucede, que algunas derivadas existen pero no para todos los ordenes pese a que
se puedan calcular con las formulas. Es necesario considerar los teoremas
expuestos en la sección de los teoremas
ECUACION BIDIMENSIONAL DEL CALOR
La ecuación bidimensional del calor describe cómo se distribuye la temperatura
en un cuerpo sólido en función del tiempo y el espacio. El interés en
su estudio radica en las múltiples aplicaciones que tiene en diversas
ramas de la ciencia. En las matemáticas generales, representa la típica
ecuación en derivadas parciales parabólica y concretamente en la estadística
está relacionada con los procesos aleatorios. Por otro lado, en el
campo de la química nos predice, entre otros procesos de transferencia
de calor, que si juntamos un material a 0º y otro a 100º, rápidamente la
temperatura del punto de conexión entre ambos será de 50º.
DE DONDE SE LA OBTIENE:
Esta ecuación se la obtiene de la forma general de una ecuación de derivadas parciales lineal y de segundo orden (EDP) con 2 variables independientes X e Y.
Si “U” representa la variable dependiente Y; y “X” e “Y” representan las variables independientes, entonces tenemos que:

donde A,B,C,...,G son funciones de x e y.
Cuando G(x,y) = 0, se dice que la ecuación es homogénea; en caso contrario se dice que es no homogénea.

DIFERENCIA TOTAL Y PARCIALES
En matematica una derivada parcial de una funcionde diversas variables, es su derivada respecto a una de esas variables manteniendo las otras como constantes. Las derivadas parciales son útiles en calculo vectorial.
La derivada parcial de una función f respecto a la variable x se representa con cualquiera de las siguientes notaciones equivalentes:
 es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
Cuando una magnitud es función de diversas variables (
es función de diversas variables ( ,
, ,
, ,
,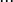 ), es decir:
), es decir:
 en un punto dado. Esta recta es paralela al plano formado por el eje de
la incógnita respecto a la cual se ha hecho la derivada y el eje z.
en un punto dado. Esta recta es paralela al plano formado por el eje de
la incógnita respecto a la cual se ha hecho la derivada y el eje z.
Analíticamente el gradiente de una función es la máxima pendiente de dicha función en la dirección que se elija. Mientras visto desde el álgebra lineal, la dirección del gradiente nos indica hacia donde hay mayor variación en la función.
Como las derivadas en una variable, las derivadas parciales están definidas como el limite . Donde U es un subconjunto abierto de Rn y f : U → R una función. Definimos derivada parcial de f en el punto a = (a1,..., an) ∈ U con respecto a la i-ésima variable xi como:
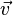 es el vector unitario del eje respecto al que se deriva (
es el vector unitario del eje respecto al que se deriva ( ).
).
Incluso si todas las derivadas parciales existen en el punto a, la función no necesariamente es continua en ese punto. Sin embargo, si todas las derivadas parciales existen alrededor de a y son continuas, entonces la función no sólo es continua sino además diferenciable cerca de a. En este caso, f es una función C1.
La derivada parcial de una función f respecto a la variable x se representa con cualquiera de las siguientes notaciones equivalentes:
Donde
 es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
es la letra 'd' redondeada, conocida como la 'd de Jacobi'.Cuando una magnitud
 es función de diversas variables (
es función de diversas variables ( ,
, ,
, ,
,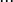 ), es decir:
), es decir:Al realizar esta derivada obtenemos la expresión que nos permite obtener la pendiente de la recta tangente a dicha función
 en un punto dado. Esta recta es paralela al plano formado por el eje de
la incógnita respecto a la cual se ha hecho la derivada y el eje z.
en un punto dado. Esta recta es paralela al plano formado por el eje de
la incógnita respecto a la cual se ha hecho la derivada y el eje z.Analíticamente el gradiente de una función es la máxima pendiente de dicha función en la dirección que se elija. Mientras visto desde el álgebra lineal, la dirección del gradiente nos indica hacia donde hay mayor variación en la función.
Como las derivadas en una variable, las derivadas parciales están definidas como el limite . Donde U es un subconjunto abierto de Rn y f : U → R una función. Definimos derivada parcial de f en el punto a = (a1,..., an) ∈ U con respecto a la i-ésima variable xi como:
O visto respecto a la derivada direccional:
donde
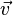 es el vector unitario del eje respecto al que se deriva (
es el vector unitario del eje respecto al que se deriva ( ).
).Incluso si todas las derivadas parciales existen en el punto a, la función no necesariamente es continua en ese punto. Sin embargo, si todas las derivadas parciales existen alrededor de a y son continuas, entonces la función no sólo es continua sino además diferenciable cerca de a. En este caso, f es una función C1.

DIFERENCIANDO
En matematica, una aproximación lineal es una aproximación de una funcion cualquiera usando una trasformacion lineal. Por ejemplo, dada una función diferenciable f de una variable real, se puede expresar (generalizada en el Teorema de Taylor) de la siguiente manera:
 es una función que representa el error usando la notacion de landau (Así,
es una función que representa el error usando la notacion de landau (Así,  tiende a 0 cuando
tiende a 0 cuando  tiende a
tiende a  ). La aproximación se obtiene al despreciar la suma de esta función error.
). La aproximación se obtiene al despreciar la suma de esta función error.
- TEOREMA DE APROXIMACION LINEAL
En matematica, una aproximación lineal es una aproximación de una funcion cualquiera usando una trasformacion lineal. Por ejemplo, dada una función diferenciable f de una variable real, se puede expresar (generalizada en el Teorema de Taylor) de la siguiente manera:
 es una función que representa el error usando la notacion de landau (Así,
es una función que representa el error usando la notacion de landau (Así,  tiende a 0 cuando
tiende a 0 cuando  tiende a
tiende a  ). La aproximación se obtiene al despreciar la suma de esta función error.
). La aproximación se obtiene al despreciar la suma de esta función error.
Para encontrar la aproximación lineal de ![\sqrt[3]{25}](http://upload.wikimedia.org/math/6/1/0/6103bcd9bd4b52da8971871123af4e9c.png) se hace lo siguiente:
se hace lo siguiente:
![\sqrt[3]{25}](http://upload.wikimedia.org/math/6/1/0/6103bcd9bd4b52da8971871123af4e9c.png) se hace lo siguiente:
se hace lo siguiente:
- Considérese la función

- Se tiene la derivada :
- Según lo ya visto,
- El resultado, 2.926, está razonablemente cerca del valor que puede dar una calculadora 2.924…
https://www.youtube.com/watch?v=a5WFxx-nRRQ
REGLA DE LA CADENA
Recuerde que con la notacion de Leibniz de la cadena para una funcion de una variable se expresa como sigue: Si y es una funcion de u y dy/du existe y su u es una funcion de x y du/dx existe, entonces es una funcion de x y dy/dx existe y esta demostrada por:
dy/dx = dy/du du/dy
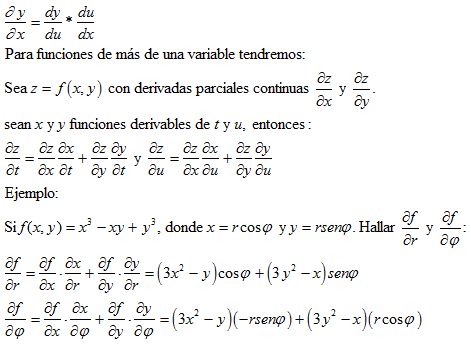
https://www.youtube.com/watch?v=YekjPMP-Mrg
DERIVADAS DE FUNCIONES IMPLICITAS

Ejemplo


https://www.youtube.com/watch?v=0Cmtdy5nkJg
https://www.youtube.com/watch?v=oneC1gsSQaM
DETERMINANTE JACOBIANO
Matriz Jacobiana
Esta matriz es notada de diversas maneras:
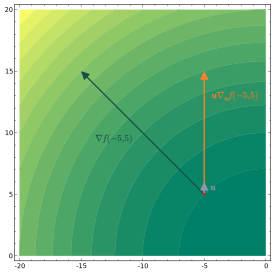
DERIVADA DIRECCIONAL
En la derivada direccional de una función multivariable sobre un vector dado, representa la tasa de cambio de la función en la dirección de dicho vector. Este concepto generaliza a las derivadas parciales, ya que estas son derivadas direccionales en los vectores paralelos a los ejes.
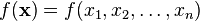
en la dirección del vector:

es la funcion definida por el limite :

 " denota el producto escalar o producto punto entre vectores. En cualquier punto
" denota el producto escalar o producto punto entre vectores. En cualquier punto  ,
la derivada direccional de f representa intuitivamente la tasa de
cambio de f con respecto al tiempo cuando se está moviendo a una
velocidad y dirección dada por
,
la derivada direccional de f representa intuitivamente la tasa de
cambio de f con respecto al tiempo cuando se está moviendo a una
velocidad y dirección dada por  en dicho punto.
en dicho punto.

 después de la normalización, ignorando así su magnitud. En este caso:
después de la normalización, ignorando así su magnitud. En este caso:
 por unidad de distancia.
por unidad de distancia.
REGLA DE LA CADENA
Recuerde que con la notacion de Leibniz de la cadena para una funcion de una variable se expresa como sigue: Si y es una funcion de u y dy/du existe y su u es una funcion de x y du/dx existe, entonces es una funcion de x y dy/dx existe y esta demostrada por:
dy/dx = dy/du du/dy
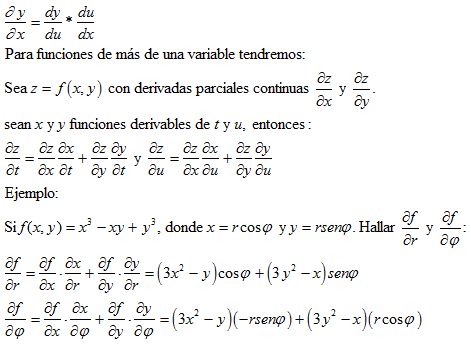
https://www.youtube.com/watch?v=YekjPMP-Mrg
DERIVADAS DE FUNCIONES IMPLICITAS
Funciones implícitas
Una correspondencia o una función está definida en forma implícita cuando no aparece despejada la y sino que la relación entre x e y viene dada por una ecuación de dos incógnitas cuyo segundo miembro es cero.Derivadas de funciones implícitas
Para hallar la derivada en forma implícita no es necesario despejar y. Basta derivar miembro a miembro, utilizando las reglas vistas hasta ahora y teniendo presente que:
x'=1.
En general y'≠1.
Por lo que omitiremos x' y dejaremos y'.
Derivar las funciones:
1.
 2.
2. 

1.




Cuando las funciones son más complejas vamos a utilizar una regla para facilitar el cálculo:
https://www.youtube.com/watch?v=0Cmtdy5nkJg
https://www.youtube.com/watch?v=oneC1gsSQaM
DETERMINANTE JACOBIANO
En calculo vectorial, se
llama jacobiano o determinante jacobiano al determinante de la matriz jacobiana. Tanto la matriz
jacobiana como el determinante jacobiano reciben su nombre en honor al
matemático Carl Gustav Jacobi.
En geometria algebraica, el jacobiano de una curva hace referencia a la variedad jacobiana, un grupo y variedad algebraica asociada a la curva, donde la curva puede ser embebida
Matriz Jacobiana
La matriz jacobiana es una matriz formada
por las derivadas parciales de
primer orden de una función. Una de las aplicaciones más interesantes de esta
matriz es la posibilidad de aproximar linealmente a la
función en un punto. En este sentido, el jacobiano representa la derivada de
una función multivariable.
Propiamente
deberíamos hablar más que de matriz jacobiana, de diferencial jacobiana o aplicación
lineal jacobiana ya que la forma de la matriz dependerá de la base o
coordenadas elegidas. Es decir, dadas dos bases diferentes la aplicación lineal
jacobiana tendrá componentes diferentes aún tratándose del mismo objeto
matemático. La propiedad básica de la "matriz" jacobiana es la
siguiente,
dada una aplicación cualquiera continua,
es decir se
dirá que
es diferenciable si existe una aplicación lineal tal
que:
Función escalar
Empecemos con el
caso más sencillo de una función escalar .
En este caso la matriz jacobiana será una matriz formada por un vector fila que
coincide con el gradienete. Si la función admite derivadas
parciales para cada variable puede verse que basta definir la
"matriz" jacobiana como:
Ya que entonces se
cumplirá la relación (1) automáticamente, por lo que en este caso la "matriz
jacobiana" es precisamente el gradiente.
Función vectorial
Supongamos es
una función que va del espacio euclídeo n-dimensional a otro espacio euclídeo
m-dimensional. Esta función
está determinada por m
funciones escalares reales:
Cuando la función
anterior es diferenciable, entonces
las derivadas parciales de estas m
funciones pueden ser organizadas en una matriz m por n, la
matriz jacobiana de F:
Esta matriz es notada de diversas maneras:
Nótese que la
fila, i-ésima fila coincidirá dada con el gradiente de la función yi,
para i = 1,...,m
Si p es un punto de Rn y F es diferenciable en p, entonces su derivada está dada por JF(p). En estecaso, la aplicación lineal descrita por JF(p) es la mejor aproximación lineal de F cerca del punto p, de esta manera:
Si p es un punto de Rn y F es diferenciable en p, entonces su derivada está dada por JF(p). En estecaso, la aplicación lineal descrita por JF(p) es la mejor aproximación lineal de F cerca del punto p, de esta manera:
para x cerca de p. O con mayor precisión:
Determinante jacobiano
Si m = n, entonces F es
una función que va de un espacio n-dimensional a otro. En este caso la matriz
jacobiana es cuadrada y podemos
calcular su determinante, conocido como el determinante jacobiano o simplemente
jacobiano.
El determinante
jacobiano en un punto dado nos da información importante sobre el
comportamiento de F cerca de
ese punto. Para empezar, una función F
es invertible cerca de p si el
determinante jacobiano en p es
no nulo. Más aún, el valor absoluto del
determinante en p nos da el
factor con el cual F expande o
contrae su volumen cerca de p.
Ejemplos
Ejemplo 1. El determinante jacobiano de la función F : R3 → R3
definida como:
es:
El teorema de la función inversa
garantiza que la función es localmente invertible en todo el dominio excepto
quizá donde ó (es decir, los valores
para los que el determinante se hace cero). Si imaginamos un objeto pequeño
centrado en el punto (1,1,1) y le aplicamos F, tendremos un objeto aproximadamente 40 veces más voluminoso que
el original.
DERIVADA DIRECCIONAL
En la derivada direccional de una función multivariable sobre un vector dado, representa la tasa de cambio de la función en la dirección de dicho vector. Este concepto generaliza a las derivadas parciales, ya que estas son derivadas direccionales en los vectores paralelos a los ejes.
Definición general
La derivada direccional de una funcion escalar:
en la dirección del vector:

es la funcion definida por el limite :
Si la función es diferenciable, puede ser escrita en término de su gradiente

donde "
 " denota el producto escalar o producto punto entre vectores. En cualquier punto
" denota el producto escalar o producto punto entre vectores. En cualquier punto  ,
la derivada direccional de f representa intuitivamente la tasa de
cambio de f con respecto al tiempo cuando se está moviendo a una
velocidad y dirección dada por
,
la derivada direccional de f representa intuitivamente la tasa de
cambio de f con respecto al tiempo cuando se está moviendo a una
velocidad y dirección dada por  en dicho punto.
en dicho punto.
Definición solo en la dirección de un vector
Algunos autores definen la derivada direccional con respecto al vector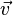 después de la normalización, ignorando así su magnitud. En este caso:
después de la normalización, ignorando así su magnitud. En este caso: por unidad de distancia.
por unidad de distancia.Restricción al vector unitario
Algunos autores restringen la definición de la derivada direccional con respecto a un vector unitario. Con esta restricción, las dos definiciones anteriores se convierten en una misma.
La determinación de los valores máximos y mínimos de una función, es
uno de los logros de la gran potencia que tiene el Cálculo. Tomemos f(x)
como una función de x. El valor de x para el cual la derivada de f(x) con respecto a x es igual a cero, corresponden a los puntos de
inflexión de la función f(x) donde sus valores son máximo y mínimo.
Por ejemplo, la altura de un proyectil que se dispara en línea recta, está dada por las ecuaciones del movimiento:
Abajo se muestra la gráfica de la altura y(t), tomando y0 = 0.

La derivada de una función puede ser interpretada geométricamente como la pendiente de curva de la función matemática y(t), representada la derivada en función de t. La derivada es positiva cuando una función es creciente hacia un máximo, cero (horizontal) en el máximo, y negativa justo después del máximo. La segunda derivada es la tasa de cambio de la primera derivada y es negativa en el proceso que se acaba de describir, puesto que la primera derivada (la pendiente), siempre es cada vez mas pequeña. La segunda derivada es siempre negativa en la "joroba" de una función, que corresponde a un máximo de la función.
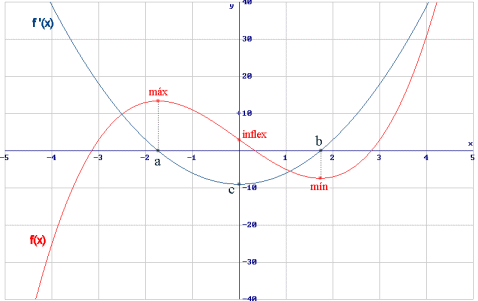
En la función simple que se ha mostrado en el ejemplo solo hay un máximo. Las funciones mas complejas pueden tener múltiples máximos y mínimos y la segunda derivada, nos proporciona la manera de distinguirlos.
https://www.youtube.com/watch?v=eh-NDkH-hXk
Maximos y Minimos absolutos
https://www.youtube.com/watch?v=2zW0qqaDtOE
INTEGRALES MULTIPLES
na integral múltiple es un tipo de integral definida aplicada a funciones de más de una variable real, por ejemplo, ó
ó 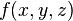

De la misma manera en que la integral de una función positiva de una variable definida en un intervalo puede interpretarse cómo el
área entre la gráfica de la función y el eje x en ese intervalo, la doble integral de una función positiva
de una variable definida en un intervalo puede interpretarse cómo el
área entre la gráfica de la función y el eje x en ese intervalo, la doble integral de una función positiva  de dos variables, definida en una región del plano xy, se puede
interpretar como el volumen entre la superficie definida por la función y
el plano xy en ese intervalo. Al realizar una "integral triple" de una
función
de dos variables, definida en una región del plano xy, se puede
interpretar como el volumen entre la superficie definida por la función y
el plano xy en ese intervalo. Al realizar una "integral triple" de una
función 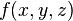 definida en una región del espacio xyz, el resultado es un hhipervolumen , sin embargo es bueno notar que si
definida en una región del espacio xyz, el resultado es un hhipervolumen , sin embargo es bueno notar que si  el resultado se puede interpretar como el volumen de la región de
integración. Para integrales de órdenes superiores, el resultado
geométrico corresponde a hipervolúmenes de dimensiones cada vez
superiores.
el resultado se puede interpretar como el volumen de la región de
integración. Para integrales de órdenes superiores, el resultado
geométrico corresponde a hipervolúmenes de dimensiones cada vez
superiores.
La manera más usual de representar una integral múltiple es anidando signos de integracion en el orden inverso al orden de ejecución (el de más a la izquierda es el último en ser calculado), seguido de la función y los diferenciales en orden de ejecución. El dominio de integración se representa sobre cada signo de integral, o a menudo es abreviado por una letra en el signo de integral de más a la derecha:

Las integrales múltiples están estrechamente relacionadas con las integrales iteradas, mismas que son necesarias para resolver las integrales múltiples. La diferencia entre integrales múltiples e iteradas consiste en que una se refiere al concepto matemático de integral (aplicado a varias variables) y otra al procedimiento por el cual se resuelve la integral múltiple. Si la expresión
 es una funcion acotada y tanto A como B son regiones acotadas también. Esto se entiende
fácilmente pensando que si la función o la región del dominio no están
acotadas, la integral múltiple no puede existir.
es una funcion acotada y tanto A como B son regiones acotadas también. Esto se entiende
fácilmente pensando que si la función o la región del dominio no están
acotadas, la integral múltiple no puede existir.
La notación
Por ejemplo:
Ya que tanto 2 sin(x) como 3y3 son funciones impares, y existe simetría tanto con respecto al eje x como con respecto al eje y, las primeras dos integrales se nulifican, de tal forma que la integral original es igual únicamente a la tercera.
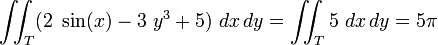
Si se utiliza una transformación que siga la relación:
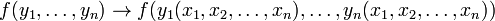 Entonces se puede utilizar el jacobiano de la transformación para simplificar la integral
Entonces se puede utilizar el jacobiano de la transformación para simplificar la integral

En un espacio R2, un dominio de integración que tenga una simetría circular
es muchas veces suceptible de ser transformado de coordenadas
rectangulares a polares, lo que significa que cada punto P (x, y) del
dominio de una integral doble tomará su valor correspondiente en
coordenadas polares mediante la siguiente transformación:
 Por ejemplo:
Por ejemplo:
El determinante jacobiano de la transformación es:
 .
.
Por lo tanto, una vez transformada la función, y multiplicada por su determinante jacobiano, ésta es igual a la integral original:
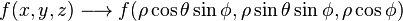
El determinante jacobiano de la transformación es el siguiente:
Por lo tanto los diferenciales dx dy dz se transforman en ρ2 sin(φ) dρ dθ dφ.
Finalmente se obtiene la fórmula de integración:
El uso de coordenadas cilindricas para transformar una integral triple, es conveniente especialmente cuando el dominio de integración presenta simetría alrededor del eje z. La función se transforma mediante la siguiente relación.
 El determinante jacobiano de la transformación es el siguiente:
El determinante jacobiano de la transformación es el siguiente:
INTEGRACION SOBRE REGIONES MAS GENERALES
https://www.youtube.com/watch?v=s-bw-mSdgRQ
TRANSFORMACION DE INTEGRALES MULTIPLES
En el cálculo de una dimensión, es frecuente que usemos un cambio de variables (o una sustitución) para simplificar una integral. Al cambiar los papeles de x y u, podemos escribir la regla de la sustitución como:
Otra forma de escribir la ecuación anterior es como sigue:
Un cambio de variables también puede ser útil en integrales dobles. Ya hemos visto esto en las transformación a coordenadas polares. Las nuevas variables r y o están relacionadas con las viejas variables x y y por las ecuaciones.
El cambo de variables entonces para una integral doble en coordenadas polares quedaría de la siguiente forma
donde "S" es la región el el plano polar que representa a la superficie "R" en el plano cartesiano.
De una forma más general podemos decir que un cambio de variables es realizado debido a una transformación T del plano (u,v) al plano (x,y)
Si T es una transformada uno a uno, entonces tiene transformada inversa Texp-1 del plano xy al plano uv, pudiendo despejar de las ecuaciones anteriores para u y v
La transformación dibuja una imagen de la superficie S utilizando sus límites.El primer lado ,S1, es cuando v=0. Utilizando las ecuaciones obtenemos que x=u², y=0, obteniendo que 0≤x≤1. Con estro trazamos en el plano xy a S1 como el segmento de recta que va de (0,0) a (0,1).
El segundo lado, S2, es cuando hacemos u=1, sustituyendo en las ecuaciones obtenemos:
Continuando con S3 (v=1) obtenemos que la representación en el playo xy corresponde a la parábola que va de (0,2) a (-1,0).
Por último al desarrollar la transformación para S4 encontramos que es el segmento de recta que va desde (-1,0) hacia (0,0).
Al identificar la superficie S nos movemos en sentido antihorario, por lo tanto al graficar en el plano xy nos moveremos en el mismo sentido, obteniendo una gráfica delimitada por dos parábolas y el eje x.
La imagen de nuestra región S es la región R en el plano xy, que tiene en uno de sus vértices con coordenadas (x0,y0)=T(u0,v0).
El vector
https://www.youtube.com/watch?v=pkDI9iKHbjs
APLICACIONES DE LAS INTEGRALES MULTIPLES
Ya hemos visto una aplicación de las integrales dobles: calcular volúmenes. Otra aplicación geométrica es hallar áreas de superficies y lo haremos en la siguiente sección. En esta sección, exploramos aplicaciones físicas como por ejemplo calcular masa, carga eléctrica, centros de masa y momento de inercia. Veremos que estas ideas físicas también son importantes cuando se aplican a funciones de densidad de probabilidad de dos variables aleatorias.
Conociendo las integrales dobles, podemos considerar una lámina con densidad variable. Supongamos que la lámina ocupa una región D del plano xy y su densidad (en unidades de masa por área unitaria) en un punto (x,y) en D está dada por ρ(x,y), donde ρ es una función continua en D. Esto significa que
Si ahora aumentamos el número de sub-rectángulos, obtenemos la masa total m de la lámina como el límite del valor de las aproximaciones:
Los físicos también consideran otros tipos de densidad que se pueden
tratar en la misma manera. Por ejemplo, si una carga eléctrica se
distribuye sobre una región D y la densidad de carga (en unidades de carga por área unitaria) está dada por σ(x,y) en un punto (x,y) en D, entonces la carga total Q está dada por
Por ejemplo, la altura de un proyectil que se dispara en línea recta, está dada por las ecuaciones del movimiento:
Abajo se muestra la gráfica de la altura y(t), tomando y0 = 0.

La derivada de una función puede ser interpretada geométricamente como la pendiente de curva de la función matemática y(t), representada la derivada en función de t. La derivada es positiva cuando una función es creciente hacia un máximo, cero (horizontal) en el máximo, y negativa justo después del máximo. La segunda derivada es la tasa de cambio de la primera derivada y es negativa en el proceso que se acaba de describir, puesto que la primera derivada (la pendiente), siempre es cada vez mas pequeña. La segunda derivada es siempre negativa en la "joroba" de una función, que corresponde a un máximo de la función.

En la función simple que se ha mostrado en el ejemplo solo hay un máximo. Las funciones mas complejas pueden tener múltiples máximos y mínimos y la segunda derivada, nos proporciona la manera de distinguirlos.
https://www.youtube.com/watch?v=eh-NDkH-hXk
Maximos y Minimos absolutos
https://www.youtube.com/watch?v=2zW0qqaDtOE
INTEGRALES MULTIPLES
na integral múltiple es un tipo de integral definida aplicada a funciones de más de una variable real, por ejemplo,
 ó
ó 

De la misma manera en que la integral de una función positiva
 de una variable definida en un intervalo puede interpretarse cómo el
área entre la gráfica de la función y el eje x en ese intervalo, la doble integral de una función positiva
de una variable definida en un intervalo puede interpretarse cómo el
área entre la gráfica de la función y el eje x en ese intervalo, la doble integral de una función positiva  de dos variables, definida en una región del plano xy, se puede
interpretar como el volumen entre la superficie definida por la función y
el plano xy en ese intervalo. Al realizar una "integral triple" de una
función
de dos variables, definida en una región del plano xy, se puede
interpretar como el volumen entre la superficie definida por la función y
el plano xy en ese intervalo. Al realizar una "integral triple" de una
función 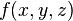 definida en una región del espacio xyz, el resultado es un hhipervolumen , sin embargo es bueno notar que si
definida en una región del espacio xyz, el resultado es un hhipervolumen , sin embargo es bueno notar que si  el resultado se puede interpretar como el volumen de la región de
integración. Para integrales de órdenes superiores, el resultado
geométrico corresponde a hipervolúmenes de dimensiones cada vez
superiores.
el resultado se puede interpretar como el volumen de la región de
integración. Para integrales de órdenes superiores, el resultado
geométrico corresponde a hipervolúmenes de dimensiones cada vez
superiores.La manera más usual de representar una integral múltiple es anidando signos de integracion en el orden inverso al orden de ejecución (el de más a la izquierda es el último en ser calculado), seguido de la función y los diferenciales en orden de ejecución. El dominio de integración se representa sobre cada signo de integral, o a menudo es abreviado por una letra en el signo de integral de más a la derecha:
Es importante destacar que no es posible calcular la funcion prmitiva o antiderivada de una función de más de una variable por lo que las integrales múltiples indefinidas no existen.

Las integrales múltiples están estrechamente relacionadas con las integrales iteradas, mismas que son necesarias para resolver las integrales múltiples. La diferencia entre integrales múltiples e iteradas consiste en que una se refiere al concepto matemático de integral (aplicado a varias variables) y otra al procedimiento por el cual se resuelve la integral múltiple. Si la expresión
 es una funcion acotada y tanto A como B son regiones acotadas también. Esto se entiende
fácilmente pensando que si la función o la región del dominio no están
acotadas, la integral múltiple no puede existir.
es una funcion acotada y tanto A como B son regiones acotadas también. Esto se entiende
fácilmente pensando que si la función o la región del dominio no están
acotadas, la integral múltiple no puede existir.La notación
Métodos de integración
Funciones constantes
En el caso de funciones constantes, el resultado es trivial: simplemente multiplíquese el valor de la función constante c por la medida del dominio de integración. Si c = 1, y es integrada a través de una región de R2 esto da el área de la región, mientras que si es una región de R3 da el volumen de la región y así sucesivamente.Por ejemplo:
-
 y
y 
- Integrando f sobre D:
Uso de simetrías
En el caso de un dominio en el que exista simetría al menos respecto de uno de los ejes, y donde la función para integrar contenga al menos una funcion impar con respecto a esa variable, la integral se vuelve nula (ya que la suma de cantidades iguales con signo opuesto es cero). Por ejemplo
Dada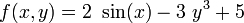 y que
y que 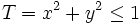 es el dominio de integración del disco de radio 1 centrado en el origen.
es el dominio de integración del disco de radio 1 centrado en el origen.
- Usando la propiedad lineal de las integrales, la integral se descompone en tres partes:
Ya que tanto 2 sin(x) como 3y3 son funciones impares, y existe simetría tanto con respecto al eje x como con respecto al eje y, las primeras dos integrales se nulifican, de tal forma que la integral original es igual únicamente a la tercera.
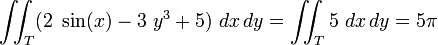
Cambio de variables
A menudo, es útil para reducir la complejidad de la integral cambiar una variable por otra que resulte más cómoda, sin embargo esto exige el cambio de la región de integración, además de añadir un factor de corrección al diferencial conocido como determinante (en valor absoluto o módulo). El cambio de una variable por otra es en un sentido geométrico, una transformación desde un espacio hasta otro, y es esta transformación la que exige estos ajustes.
Si se utiliza una transformación que siga la relación:
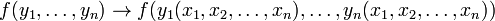 Entonces se puede utilizar el jacobiano de la transformación para simplificar la integral
Entonces se puede utilizar el jacobiano de la transformación para simplificar la integralCoordenadas Polares

La transformación de coordenadas rectangulares a polares. Se puede notar
que el área de la región polar es distinta que la de la región
rectangular, lo que justifica la necesidad del jacobiano. También se
puede demostrar que si se consiera 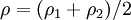 (el radio medio), el área de la región polar es efectivamente
(el radio medio), el área de la región polar es efectivamente  .
.
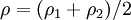 (el radio medio), el área de la región polar es efectivamente
(el radio medio), el área de la región polar es efectivamente  .
. Por ejemplo:
Por ejemplo:- Si la función es

- aplicando la transformación se obtiene la función fácilmente integrable con respecto a
 y a
y a  .
.
- Si la función es

- Uno tiene:
El determinante jacobiano de la transformación es:
 .
.Por lo tanto, una vez transformada la función, y multiplicada por su determinante jacobiano, ésta es igual a la integral original:
Coordenadas Esféricas
Cuando existe simetría esférica en un dominio en R3, es posible utilizar una transformación hacia coordenadas esféricas para simplificar una integral triple. La función es transformada por la relación: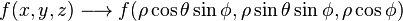
El determinante jacobiano de la transformación es el siguiente:
Por lo tanto los diferenciales dx dy dz se transforman en ρ2 sin(φ) dρ dθ dφ.
Finalmente se obtiene la fórmula de integración:
Coordenadas Cilíndricas
El uso de coordenadas cilindricas para transformar una integral triple, es conveniente especialmente cuando el dominio de integración presenta simetría alrededor del eje z. La función se transforma mediante la siguiente relación.
 El determinante jacobiano de la transformación es el siguiente:
El determinante jacobiano de la transformación es el siguiente:INTEGRACION SOBRE REGIONES MAS GENERALES
https://www.youtube.com/watch?v=s-bw-mSdgRQ
TRANSFORMACION DE INTEGRALES MULTIPLES
En el cálculo de una dimensión, es frecuente que usemos un cambio de variables (o una sustitución) para simplificar una integral. Al cambiar los papeles de x y u, podemos escribir la regla de la sustitución como:
Otra forma de escribir la ecuación anterior es como sigue:
Un cambio de variables también puede ser útil en integrales dobles. Ya hemos visto esto en las transformación a coordenadas polares. Las nuevas variables r y o están relacionadas con las viejas variables x y y por las ecuaciones.
El cambo de variables entonces para una integral doble en coordenadas polares quedaría de la siguiente forma
donde "S" es la región el el plano polar que representa a la superficie "R" en el plano cartesiano.
De una forma más general podemos decir que un cambio de variables es realizado debido a una transformación T del plano (u,v) al plano (x,y)
-
- T(u,v)=(x,y) donde x y y están relacionadas con u y v mediante las ecuaciones
-
- x=g(u,v) y=h(u,v)
Si T es una transformada uno a uno, entonces tiene transformada inversa Texp-1 del plano xy al plano uv, pudiendo despejar de las ecuaciones anteriores para u y v
-
- u=G(x,y) v=H(x,y)
Ejemplo #01
Si x=U^2+V^2 y Y= UV encuentre la imagen de el cuadradoLa transformación dibuja una imagen de la superficie S utilizando sus límites.El primer lado ,S1, es cuando v=0. Utilizando las ecuaciones obtenemos que x=u², y=0, obteniendo que 0≤x≤1. Con estro trazamos en el plano xy a S1 como el segmento de recta que va de (0,0) a (0,1).
El segundo lado, S2, es cuando hacemos u=1, sustituyendo en las ecuaciones obtenemos:
- x=1-v2 y=2v
Continuando con S3 (v=1) obtenemos que la representación en el playo xy corresponde a la parábola que va de (0,2) a (-1,0).
Por último al desarrollar la transformación para S4 encontramos que es el segmento de recta que va desde (-1,0) hacia (0,0).
Al identificar la superficie S nos movemos en sentido antihorario, por lo tanto al graficar en el plano xy nos moveremos en el mismo sentido, obteniendo una gráfica delimitada por dos parábolas y el eje x.
Cambios de variable en integrales dobles
Ahora veremos como se ve afectada un integral doble con un cambio de variable. Empezaremos con un pequeño rectángulo S en el plano uv cuya esquina inferior izquierda es el punto (u0,v0) y que tiene dimensiones Δu y Δv.La imagen de nuestra región S es la región R en el plano xy, que tiene en uno de sus vértices con coordenadas (x0,y0)=T(u0,v0).
El vector
- Sabemos lo siguientepor lo que podemos concluir que de igual manera podemos decir que Esto significa que podemos aproximar R a través del paralelogramo formado por los vectores y . Por lo tanto podemos aproximar el área de la región R como el área de este nuevo paralelogramo.
https://www.youtube.com/watch?v=pkDI9iKHbjs
APLICACIONES DE LAS INTEGRALES MULTIPLES
Ya hemos visto una aplicación de las integrales dobles: calcular volúmenes. Otra aplicación geométrica es hallar áreas de superficies y lo haremos en la siguiente sección. En esta sección, exploramos aplicaciones físicas como por ejemplo calcular masa, carga eléctrica, centros de masa y momento de inercia. Veremos que estas ideas físicas también son importantes cuando se aplican a funciones de densidad de probabilidad de dos variables aleatorias.
Conociendo las integrales dobles, podemos considerar una lámina con densidad variable. Supongamos que la lámina ocupa una región D del plano xy y su densidad (en unidades de masa por área unitaria) en un punto (x,y) en D está dada por ρ(x,y), donde ρ es una función continua en D. Esto significa que



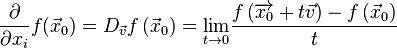




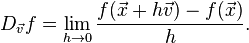

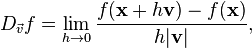




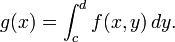



![\int_{[a,b]\times[c,d]} f(x,y)\,dx\,dy](http://upload.wikimedia.org/math/6/9/7/697484c41df80f747d04278f95ec9c2d.png)

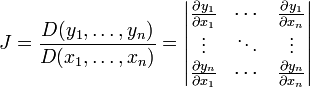







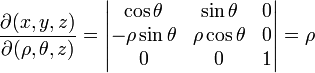








No hay comentarios:
Publicar un comentario